Tim Sort 등장배경
$C × nlogn + α$ 정렬들에 참조 지역성 원리를 적용하면
- 힙 정렬은 한 위치에 있는 요소를 해당 요소의 인덱스 두 배 또는 절반인 요소와 반복적으로 비교하기에 $C$값이 크므로 참조 지역성이 좋지 않다.
- 병합 정렬은 참조 지역성 원리는 어느 정도 만족하나, 추가 메모리가 필요하다는 단점이 있다.
- 퀵 소트의 경우 피벗 주변에서 데이터가 이동하므로 참조 지역성이 좋으며 추가 메모리도 불필요하나, 피벗을 선정하는 방법에 따라 최악의 경우 $O(n2)$의 시간 복잡도를 가질 수 있다.
이와 같이 모든 정렬 알고리즘에 장단점이 있으므로, 상수 $C$의 값이 너무 커지지 않게 동작하면서, 추가 메모리도 많이 사용하지 않고, 최악의 경우에도 $O(nlong)$으로 동작하는 정렬 알고리즘이 필요했습니다.
Tim Sort 개념
- 삽입 정렬(Insert Sort)과 병합 정렬(Merge Sort)을 결합하여 만든 정렬
- 최선의 시간 복잡도는 $O(N)$, 평균은 $O(nlogn)$이며, 최악의 경우에도 $O(nlogn)$의 시간 복잡도를 가짐
- 추가 메모리를 사용하지만 기존의 병합 정렬에 비해 적은 추가 메모리를 사용함
Insert Sort를 결합한 이유
삽입 정렬은 $O(n^2)$의 시간 복잡도를 가지지만 인접한 메모리와 비교하기 때문에 참조 지역성의 원리를 잘 만족하고 있습니다. 따라서 $n$이 작을 경우 퀵 정렬보다도 빠릅니다. 이를 이용하여 전체를 작은 덩어리로 잘라 각각을 삽입 정렬로 정렬한 뒤 병합하면 더 빠르지 않을까 하는 것이 Tim Sort의 기본 아이디어입니다.
Tim Sort 과정
- 리스트를 $2^x$개씩 자른다.
- 이때 잘린 덩어리를 run이라고 부른다.
- $2^x$는 minrun이라 부르며, 전체 원소의 개수가 $N$일 때 minrun의 크기는 $min(N, 2^5∼2^6)$으로 정의한다. run의 개수가 2의 거듭제곱이 되도록 유동적으로 minrun의 값을 정한다.
- $2^x$개까지 삽입 정렬을 진행하고, 그 이후의 원소에 대해서 가능한 크게 덩어리를 만든다.
- 인접한 run을 병합 정렬을 통해 정렬한다.
Tim Sort의 최적화 기법
Run
하나의 run을 크게 만들수록 병합 횟수가 줄어듭니다. 따라서 $2^x$개씩 삽입 정렬로 정렬하되, 그 이후 원소는 삽입 정렬을 진행하지 않고 최대한 run을 크게 만듭니다.
먼저 맨 앞의 두 원소를 비교하여 해당 run이 증가하는 덩어리인지 감소하는 덩어리인지 결정합니다. 그 후 덩어리가 $2^x$가 될 때까지 삽입 정렬을 진행합니다. 이어서 덩어리를 최대한 크게 만들기 위해 뒤의 원소 또한 증가 혹은 감소한다면 해당 덩어리에 포함시킵니다. 이 때는 삽입 정렬을 사용하지 않고 앞 원소와 비교만 진행합니다.
이후 감소하는 run은 뒤집어서 모든 run이 증가하는 run이 되도록 변환합니다.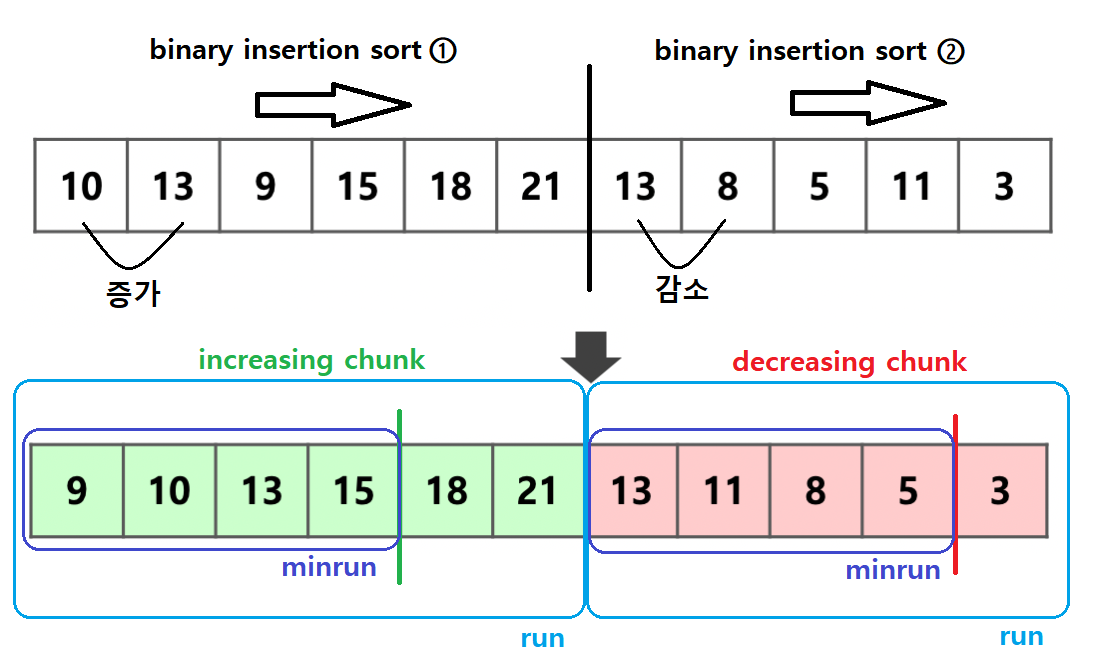 
Binary Insertion Sort
Tim Sort에서는 이진 삽입 정렬을 사용합니다. 이진 탐색은 앞의 원소들은 모두 정렬되어 있다는 전제를 기반으로 탐색하므로, 참조 지역성은 떨어지지만 $O(logn)$번의 비교를 진행하므로 조금 더 시간을 절약할 수 있습니다.
Merge
만들어진 run을 병합 정렬할 경우 최대한 크기가 비슷한 run끼리 병합해야 메모리와 시간을 절약할 수 있습니다.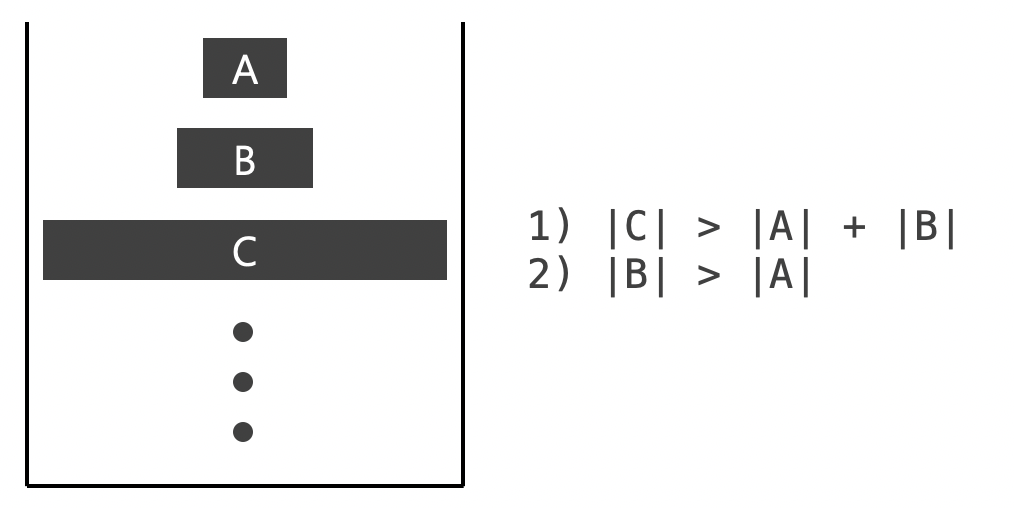 
이를 위해 하나의 run이 만들어질 때마다 스택에 담습니다. 이때 run을 스택에 push할 때마다 스택의 상위 3개의 run이 위의 두 조건을 만족해야 합니다. 만약 조건을 만족하지 않으면 $B$는 $A$와 $C$ 중 작은 run과 병합합니다.
위의 방법으로 병합할 두 run을 알아낸 후에는 병합 정렬의 가장 큰 단점인 추가 메모리 $n$ 사용을 효율적으로 해결해야 합니다.
먼저 두 개의 run중 크기가 더 작은 run을 복사하고, 각 run의 시작 혹은 끝 부분부터 크기 비교를 하여 작은 순서대로 앞을 채우면서 병합을 진행합니다. 이 경우 두 run 중 크기가 작은 run을 담을 메모리가 필요하므로 $n/2$의 추가 메모리만 사용해도 병합을 진행할 수 있습니다.
Galloping
Galloping은 병합 과정에서 추가로 사용되는 최적화 방법입니다.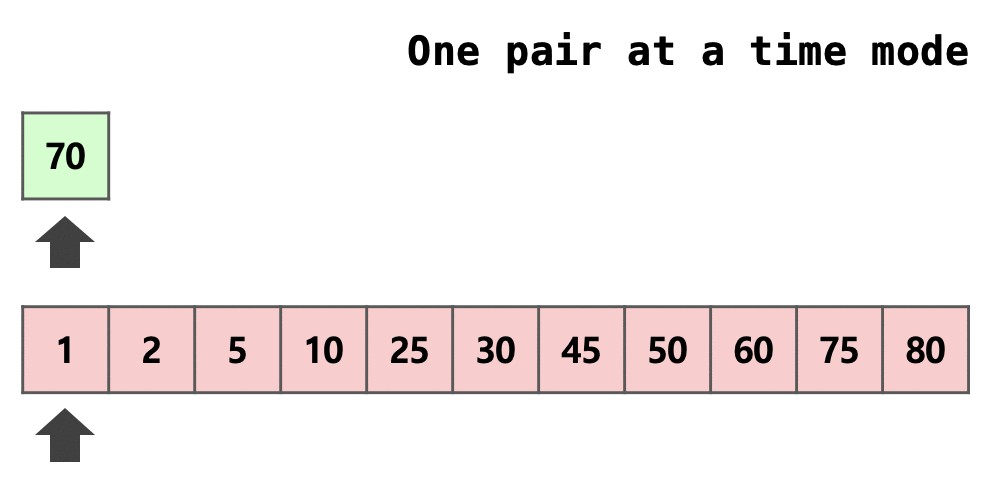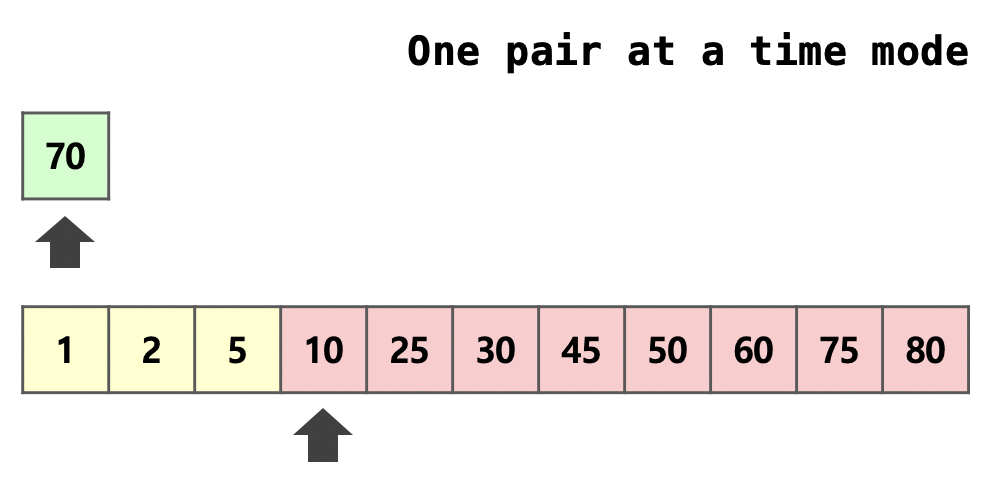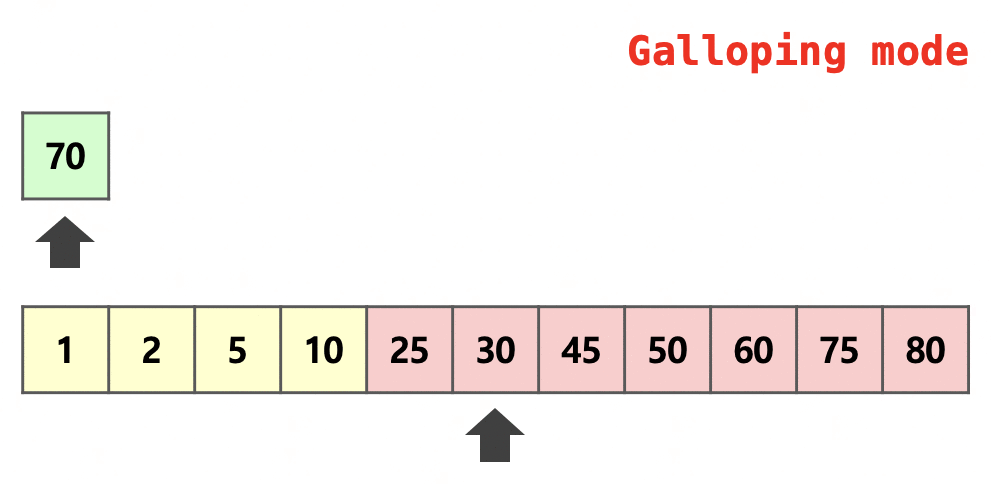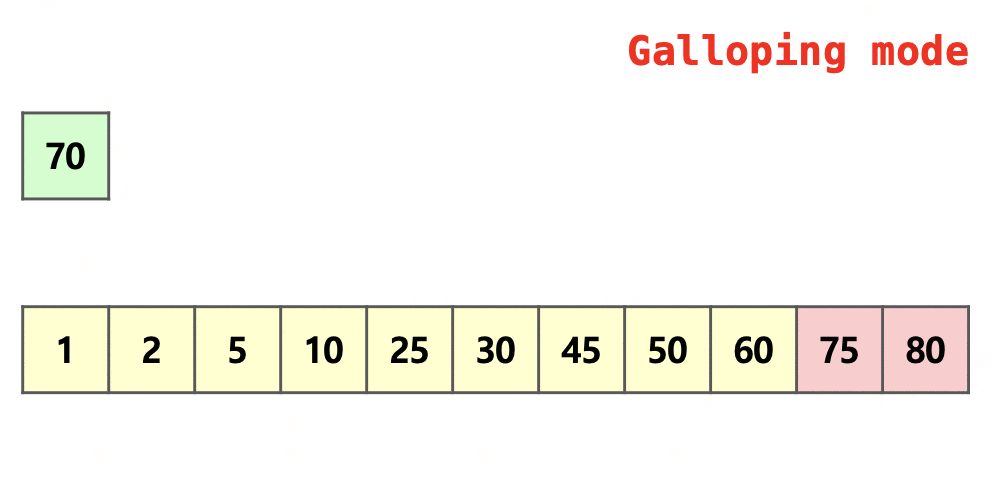 
무작위적이지 않은 실생활 데이터의 특성을 이용하여 MIN_GALLOP번 연속으로 한 run에서 병합되었을 경우 galloping mode로 전환하여 $2^k$개씩 뛰어 넘으며 대소 비교를 진행합니다. 더 이상 선택되지 않는 부분을 만났을 경우 그 이전의 지점과 그 지점 사이의 범위에서만 이분 탐색을 진행하여 어디까지 병합할지를 결정합니다.
실제 사용에서는 galloping mode에 들어가는 횟수가 많으면 MIN_GALLOP은 감소하고, 아닐 경우 증가하여 더 효율적으로 동작하도록 진행합니다.